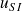Identification d'un second ordre oscillant
Un système du second ordre en régime pseudo-périodique (oscillant) possède une fonction de transfert de la forme :
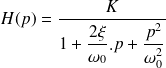avec
.
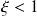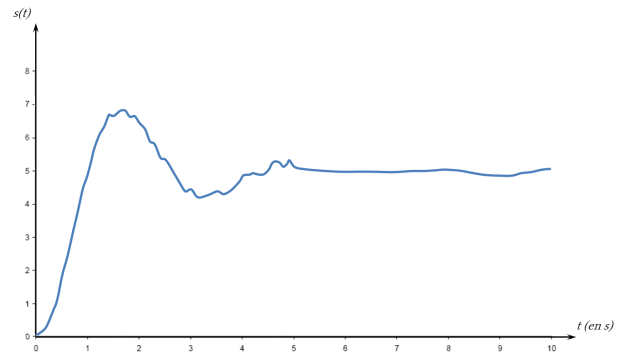
La réponse à un échelon d'amplitude
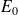d'un tel système a l'allure suivante :
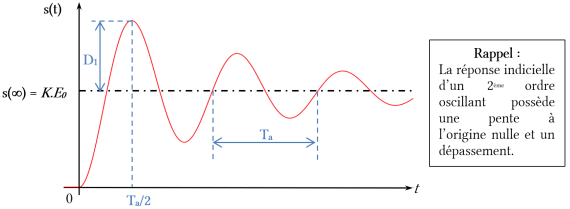
Le gain statique K peut être déterminé en relevant la valeur finale :
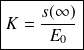
Le coefficient d'amortissement
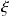peut être déterminé en relevant le premier dépassement :
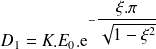ou de préférence avec le premier dépassement relatif :
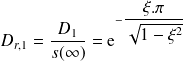. En effet, connaissant
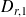, il vient :
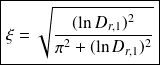
La pulsation propre du système non amorti
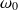peut être déterminée en relevant la pseudo-période
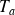ou bien le temps de premier dépassement
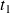(avec
) :
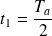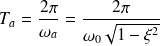donc
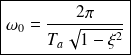ou encore
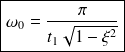
La pulsation propre peut aussi être déterminée grâce à l'abaque des temps de réponse à 5% réduits. Il convient de relever
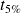expérimentalement et de connaître
.
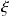Une fois les caractéristiques déterminées, il convient de tracer la réponse théorique et de la comparer à la courbe expérimentale afin de valider le modèle choisi.
Exemple :
Déterminer les caractéristiques de la fonction de transfert du système suivant, dont la réponse expérimentale à une entrée en échelon d'amplitude 2,5
est donnée ci-dessous :
