Identification d'un second ordre apériodique
Un système du second ordre en régime apériodique (sans dépassement) possède une fonction de transfert pouvant se mettre sous la forme :
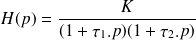avec
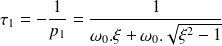et
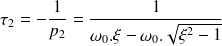
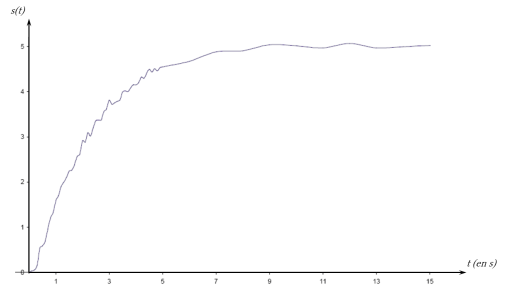
La réponse à un échelon d'amplitude
d'un système du second ordre apériodique a l'allure suivante :
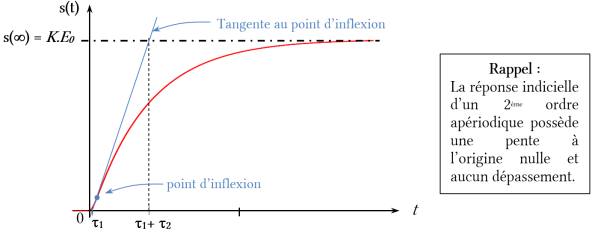
Le gain statique K peut être déterminé en relevant la valeur finale :
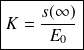
Les constantes de temps τ1 et τ2 peuvent être déterminées de manière approchée grâce à la méthode de la tangente au point d'inflexion (cette courbe possède un et un seul point d'inflexion) :
Les intersections de cette tangente avec l'axe des abscisses et l'asymptote finale donnent
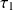et
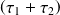.Cette méthode fonctionne bien lorsque
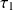et
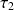sont suffisamment éloignés.Lorsque
(
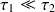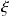grand), le comportement du système peut être approximé par un 1er ordre de constante de temps
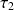, retardé d'une durée
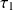. On a alors :
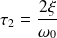
Une fois les caractéristiques déterminées, il convient encore une fois de tracer la réponse théorique et de la comparer à la courbe expérimentale afin de valider le modèle choisi.
Exemple :
Déterminer les caractéristiques de la fonction de transfert du système suivant, dont la réponse expérimentale à une entrée en échelon d'amplitude 2,5
est donnée ci-dessous :
