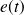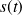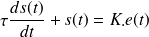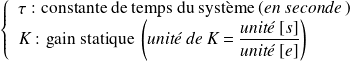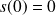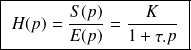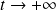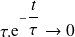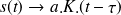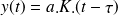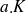C02_P1 : Modélisation et analyse temporelle des SLCI

Afficher le planAfficher le plan

Système du premier ordre

Fondamental

Un système physique d'entrée et de sortie est du 1er ordre, s'il est régi par une équation différentielle du 1er ordre à coefficients constants du type :

avec

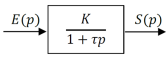Si les conditions initiales sont nulles ( ), la fonction de transfert sous forme canonique s'écrit :

Réponse indicielle

L'entrée est définie par un échelon d'amplitude :

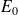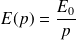
La sortie a donc pour expression dans le domaine de Laplace :

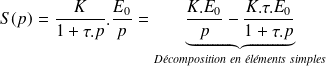
La réponse temporelle s'écrit alors :

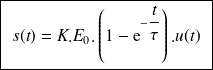
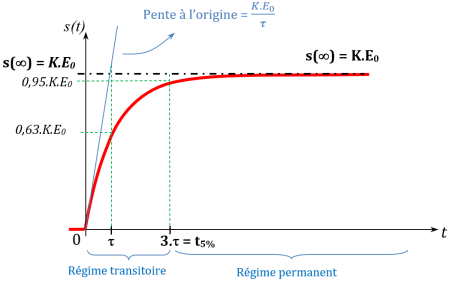
  • Valeur finale : ordonnée en  :

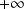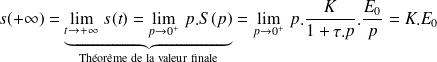
s(+\infty)= \underbrace{\lim\limits_{t\rightarrow +\infty } \, s(t) =\lim\limits_{p\rightarrow 0^+ } \,p.S(p)}_{\text{Théorème de la valeur finale}}=\lim\limits_{p\rightarrow 0^+ } \,p.\frac K {1+\tau.p}. \frac{E_0}p=K.E_0

  • Pente à l'origine :

s'(0^+)= \underbrace{\lim\limits_{t\rightarrow 0^+ } \, s'(t) =\lim\limits_{p\rightarrow +\infty } \,p.\overbrace{\left[p.S(p)\right]}^{\text{Transformée de la dérivée}}}_{\text{Théorème de la valeur initiale}}=\lim\limits_{p\rightarrow +\infty } \,p^2.\frac K {1+\tau.p}. \frac{E_0}p=\frac{K.E_0}\tau

  • Temps de réponse à 5%, :

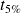On cherche 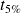tel que :

s(t_{5\%} )=0,95.s(+\infty)=0,95.K.E_0

Soit :

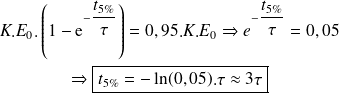
\begin{eqnarray*} &K.E_0.\left( 1-\text e^{-\frac{t_{5\%}}\tau} \right)=0,95.K.E_0 \Rightarrow e^{-\frac{t_{5\%}}\tau} =0,05\\ &\Rightarrow\boxed{t_{5\%}=-\ln(0,05).\tau\approx 3\tau} \end{eqnarray*}

  • Réponse à :

s(\tau)=K.E_0.\left(1-\text e^{-1}\right)=0,63.K.E_0

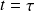  • Erreur statique:

\varepsilon_S= \varepsilon(+\infty)= \lim\limits_{t\rightarrow +\infty } \left[ \, e(t)-s(t) \, \right] =\lim\limits_{p\rightarrow 0^+ } p.\left[ \, \frac {E_0} p - \frac K {1+\tau.p}.\frac{E_0}p \, \right] =E_0.(1-K)

Réponse impulsionnelle

L'entrée est définie par une impulsion de Dirac :

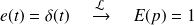
La sortie a donc pour expression dans le domaine de Laplace :

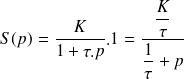
La réponse temporelle s'écrit :

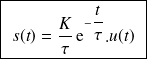
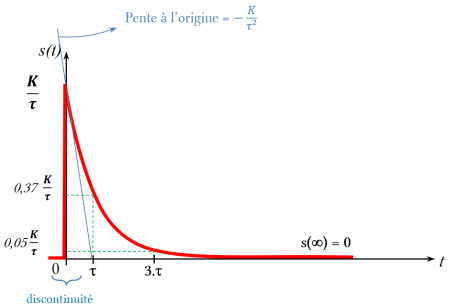
Réponse à une rampe

L'entrée est définie par une rampe :

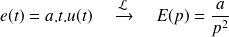
La sortie a donc pour expression dans le domaine de Laplace :

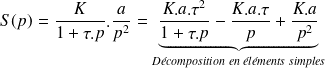
La réponse temporelle s'écrit :

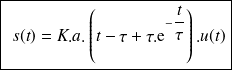
  • Valeur finale : ordonnée en  :

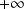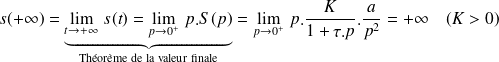
s(+\infty)= \underbrace{\lim\limits_{t\rightarrow +\infty } \, s(t) =\lim\limits_{p\rightarrow 0^+ } \,p.S(p)}_{\text{Théorème de la valeur finale}}=\lim\limits_{p\rightarrow 0^+ } \,p.\frac K {1+\tau.p}. \frac a {p^2}=+\infty \quad (K>0)

  • Pente à l'origine :

s'(0^+)= \underbrace{\lim\limits_{t\rightarrow 0^+ } \, s'(t) =\lim\limits_{p\rightarrow +\infty } \,p.\overbrace{\left[p.S(p)\right]}^{\text{Transformée de la dérivée}}}_{\text{Théorème de la valeur initiale}}=\lim\limits_{p\rightarrow +\infty } \,p^2.\frac K {1+\tau.p}. \frac a {p^2}=0

  • Etude asymptotique en :

Lorsque , le terme . Par conséquent, . L'asymptote a donc pour équation . Elle coupe l'axe des abscisses à et a pour pente :

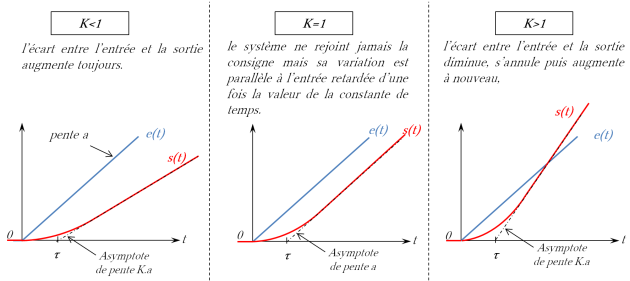
  • Erreur de trainage:

\varepsilon_v= \varepsilon(+\infty)= \lim\limits_{t\rightarrow +\infty } \left[ \, e(t)-s(t) \, \right] =\underbrace{\lim\limits_{t\rightarrow +\infty } \left[ \, a.t.(1-K).u(t) \right]}_{\text{dépend de la valeur de K}}+K .a .\tau
PrécédentPrécédentSuivantSuivant
AccueilAccueilImprimerImprimerRéalisé avec Scenari (nouvelle fenêtre)