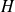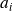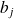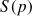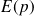C02_P1 : Modélisation et analyse temporelle des SLCI

Cours

Fonction de transfert (ou transmittance) d'un SLCI

Ci-dessous, l'équation différentielle générale à laquelle répondent les SLCI (voir chapitre précédent), reliant la grandeur d'entrée 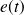à la sortie 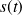du système ( ):

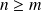$a_0.s(t) \, + \, a_1.\frac {ds(t)}{dt}\, + \, a_2.\frac {d^2s(t)}{dt^2}+...+\, a_n.\frac {d^ns(t)}{dt^n} \quad = \quad b_0.e(t)\, + \, b_1.\frac {de(t)}{dt}+...+\,b_m.\frac {d^me(t)}{dt^m}$

On peut calculer la transformation de Laplace des membres de gauche et de droite, qui, grâce à la linéarité de la transformation de Laplace, s'écrit :

$a_0.\mathcal{L}\left[s(t)\right]+ a_1.\mathcal{L}\left[\frac {ds(t)}{dt}\right] +...+a_n.\mathcal{L}\left[\frac {d^ns(t)}{dt^n}\right] =b_0.\mathcal{L}\left[e(t)\right]+ ...+b_m.\mathcal{L}\left[\frac {d^me(t)}{dt^m}\right]$

Par application du théorème de dérivation (avec conditions initiales nulles) :

$\begin{eqnarray*} a_0.S(p) \, + \, a_1.p.S(p) \, + +...+\, a_n.p^n.S(p) \quad & = & \quad b_0.E(p)\, + \, b_1.p.E(p)+...+\,b_m.p^m.E(p)\\ \\ \Rightarrow S(p). \left[a_0+a_1.p+...+a_n.p^n\right] \quad & = & \quad E(p) \left[b_0+b_1.p+...+b_m.p^m\right] \end{eqnarray*}$

Enfin :

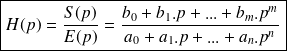
$\boxed{H(p) =\frac{S(p)}{E(p)} = \frac{ b_0+b_1.p+...+b_m.p^m}{a_0+a_1.p+...+a_n.p^n}}$

Fondamental :

La fonction ainsi obtenue est appelée transmittance ou encore fonction de transfert du système.

Il s'agit d'une fraction rationnelle (rapport de deux polynômes) en (la variable de Laplace) et de coefficients et réels.

La sortie est alors définie comme le produit de l'entrée par la fonction de transfert .

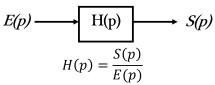Le comportement d'un système peut être entièrement défini à partir de sa fonction de transfert, plus précisément à partir des pôles (racines du dénominateur) et des zéros (racines du numérateur) de sa fonction de transfert H(p).

Complément : Notion de classe

Dans le cas où certains coefficients 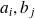sont nuls (dont 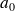), la fonction de transfert 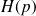d'un système linéaire continu invariant peut se mettre sous la forme :

$H(p) =\frac{S(p)}{E(p)} = \frac 1 {p^\alpha} \,\frac{ \lambda_0+\lambda_1.p+...+\lambda_l.p^l}{\mu_0+\mu_1.p+...+\mu_k.p^k} \quad \text{ avec } \lambda_0\neq 0 \text{ et } \mu_0\neq 0$

Le degré du dénominateur : 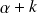représente l'ordre du système.

La puissance 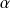de la variable de Laplace 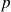isolée au dénominateur représente la classe du système.

Accueil

Imprimer