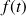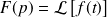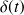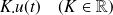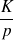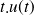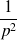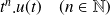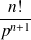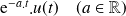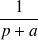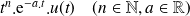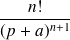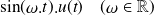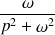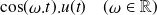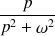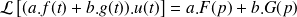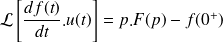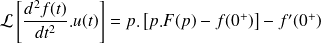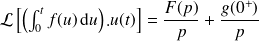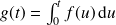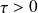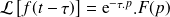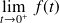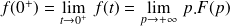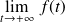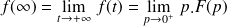Transformée de Laplace
Définition
Fondamental :
Soit une fonction
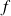telle que
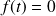pour tout
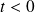(fonction causale). La transformée de Laplace de cette fonction est définie par :
![\boxed{\quad\mathcal{L}\left[f(t)\right] = F(p) =\int_{0}^{+\infty} f(t)\, \text{e}^{-p.t} \, \mathrm{d}t\quad }](../res/transfoL.png)
Remarque :
La transformée de Laplace permet de passer du domaine temporel au domaine dit de Laplace.
F(p) existe si l'intégrale existe et converge. Dans les cas rencontrés en SII, les conditions d'existence et de convergence seront réunies.
La variable
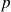est un nombre complexe (en
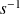). La transformée de Laplace se note par une majuscule quand cela est possible :
,
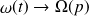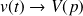. Cependant, on confond parfois les notations si la grandeur originelle est déjà en majuscule :
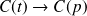pour les couples par exemple.
Exemple :
Calcul de
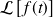avec
.
![\mathcal{L}\left[f(t)\right]=\mathcal{L}\left[K.u(t)\right]=\displaystyle{\int_{0}^{+\infty}} K.\, \text{e}^{-p.t} \, \mathrm{d}t = K.\int_{0}^{+\infty} \, \text{e}^{-p.t} \, \mathrm{d}t=K.\left[ -\frac {1}{p} \text{e}^{-p.t}\right]^{+\infty}_{0} =\frac K p](../res/transfo_echelon.png){kind=small}
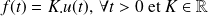Remarque : dans la pratique, les transformées de Laplace des fonctions usuelles ne se recalculeront pas. Il faudra les connaître par cœur.
Transformée de Laplace des fonctions usuelles
Les transformées de Laplace ci-dessous sont à connaître par cœur :
|
|
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Propriétés de la transformée de Laplace
Les propriétés et théorèmes ci-dessous sont à connaître par cœur :
Linéarité |
|
|---|---|
Dérivée |
|
Dérivée seconde |
|
Intégration |
|
Théorème du retard | Soit
|
Théorème de la valeur initiale | Soit
|
Théorème de la valeur finale | Soit
|
Attention :
La transformée de Laplace d'un produit n'est pas le produit des transformées de Laplace (ce serait comme écrire que l'intégrale du produit est le produit des intégrales).
