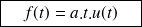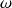Signaux tests
Pour étudier le comportement d'un système asservi d'un point de vue expérimental et tester ses performances, on soumet ce système à des signaux tests. On utilise majoritairement les modèles de signaux décrits ci-après.
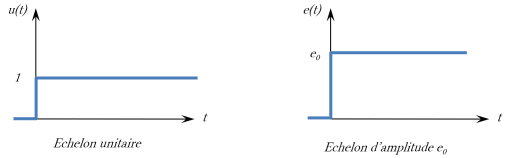
Échelon unité u(t)
Cette fonction modélise un signal qui passe de
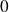à
en une durée infiniment courte et qui reste ensuite à
.
![\boxed{ \; u(t) = \left \{\begin{array}{l} 0 \quad , \forall t \in \left]-\infty, 0 \right[ \\ 1 \quad , \forall t \in \left[ 0, +\infty \right[ \\ \end{array}\right . }](../res/echelon_u.png)
On peut également décider d'imposer un échelon d'amplitude quelconque
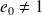. Dans ce cas la fonction d'entrée s'écrit
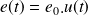
La réponse d'un système à un échelon s'appelle une réponse indicielle.
Remarque : Fonction causale
Pour rendre causale une fonction quelconque, on la multiplie par l'échelon unité :
.
Exemple : « sinus causal » =
.
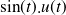Les théorèmes étudiés par la suite ne s'appliqueront que pour des fonctions causales. Si une fonction n'est pas causale, il suffira donc de la multiplier par
.
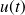Impulsion unitaire et impulsion de Dirac
On appelle impulsion unitaire la fonction
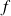définie par :
![\boxed{ \quad f(t) = \left \{\begin{array}{l} \frac 1 \lambda \quad , \forall t \in [0,\lambda]\\ 0 \quad , \forall t \notin [0,\lambda] \\ \end{array}\quad, \lambda >0\right .}](../res/dirac.png)
On obtient l'impulsion de Dirac en faisant tendre
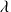vers
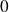. Ceci revient à générer un signal d'amplitude infinie pendant un temps nul. Ce signal est utilisé pour modéliser les chocs que peut recevoir un système.
La réponse d'un système à une impulsion de Dirac s'appelle une réponse impulsionnelle.
Rampe v(t)
Le signal rampe est utilisé pour caractériser la capacité d'un système à suivre une consigne non constante. La fonction rampe correspond mathématiquement à la primitive d'un échelon.
|  |
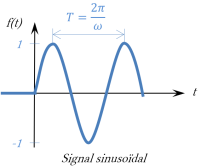
Signal sinusoïdal
Cette entrée sert à caractériser le comportement fréquentiel d'un système.
|  |
